作者最近在处理一些星点非常密集的图片时发现通过常规流程:先反卷积后去星的方法会产生令人非常不愉快的效果。SXT在线性状态下去星会使得背景非常“坑坑洼洼”的。

(此为一张缩略图,不仅光晕没有去除干净还留下了去除过量的痕迹)
因之前处理时并没有遇到过这种情况,作者怀疑是否是BXT4.0或者反卷积对星点有影响。但通过反复实验,可以确认与BXT无关,并且无论怎么调节BXT的参数,都无法让后一步的SXT在线性状态下产生一个比较好的结果。
其实,如果最后出图时选择将星点贴回,这种效果并不会影响最后出图质量。但如果想要出一张没有星点的,比较“纯净”的照片,这种去星效果就是无法忍受的。
因此为了得到一张背景干净的去星照片,作者通过多次尝试,得到了一个比较完善的办法。
一、所需插件以及脚本等
SXT,GHS,Pixelmath
二、基本原理以及实现方法
(一)基本原理
SXT在非线性状下的运行结果要明显优于在线性状态下的结果,基于此,作者设想能够在反卷积后将图片拉伸到非线性状态,利用SXT去除星点再将图片“返回”到线性状态。偶然间想到GHS可以实现上述“返回”线性的操作。
基于GHS的invert操作可以使invert 后的拉伸函数与原来的函数互为反函数,以抵消这个函数的作用。


(获取一张亮度梯度图)


(使用GHS拉伸)


(点击Invert作用于刚才的梯度图)
可以看出基本没有区别,若使用Pixelmath两张互相减去则得到两张纯黑的图,基本可以证明两张图片一摸一样,也可以证明两个函数互为反函数。
因此其基本流程为:
1. “除了降噪外一切可以在去星前完成的操作”,例如背景平衡,Linerefit,反卷积等
2. 拉伸到非线性
3. 利用SXT去星
4. 通过“历史记录”中的拉伸操作“返回”线性状态
(二)具体操作过程
1. 得到一张准备去星的照片


2. 使用GHS拉伸线性图到非线性状态

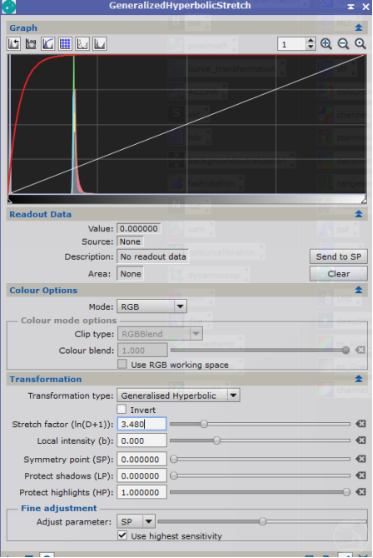
可以仅使用GH函数和线性函数做到“拉伸”“切除”,反复几次得到一张非线性图。

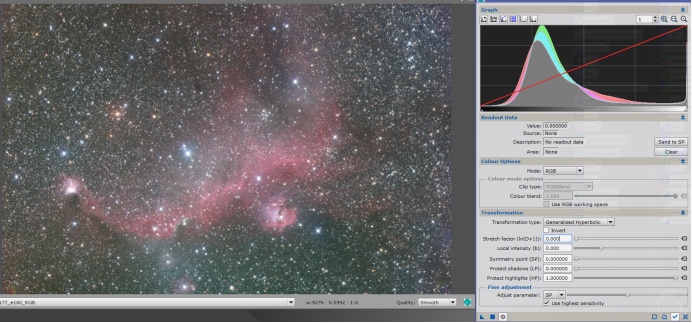
注:(1)经过多次尝试,拉伸效果对最后去星有很大的影响,这里建议拉伸的比较猛烈一些,让星点周围的光晕能够尽可能的与背景分开。若拉伸时星点亮度溢出也无所谓,只需保证主体结构没有溢出即可。

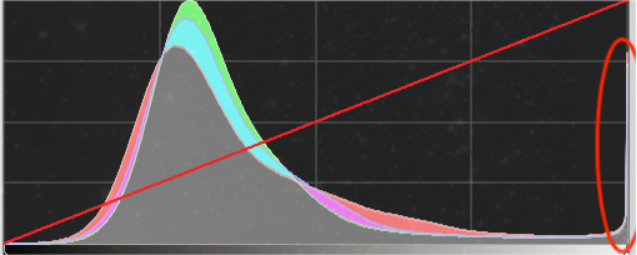
(图中画圈部分为溢出的数据,但基本都为亮星,因此无需在意)
(2)切除时要注意不能切除太多的数据,这些数据无法在后续“返回”线性的操作中恢复。
3. 使用SXT去星

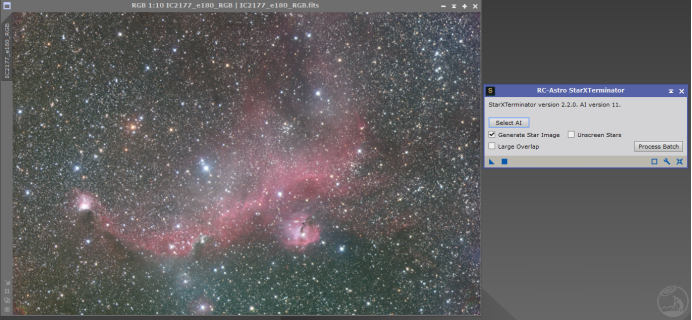
注:AI最好选择V11,选择lite或者nonoise会使背景噪声分布有明显差异,影响观感。




(去星后的图,可以看出效果还是可以接受的)
得到的星点图可以直接删除,之后可以使用Pixelmath得到星点图
4. 打开“历史记录”,从中从下到上依次拖出拉伸时的历史记录,双击后点击其中的“invert”,将其依次作用在去星图上,得到最终的“线性图”。
(若没有“History Explorer”可按Ctrl+Alt+H)

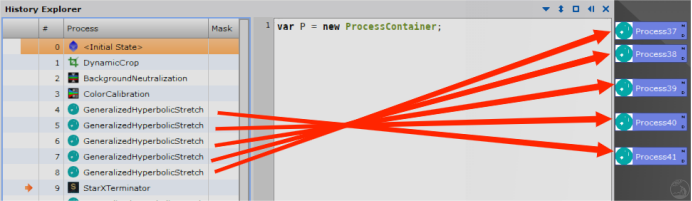
依次拖出作用函数

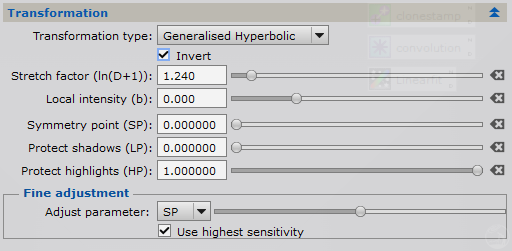
点击Invert

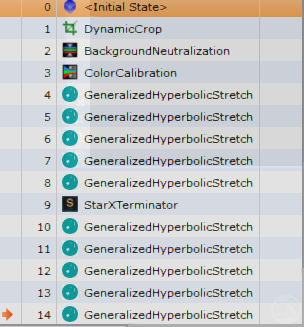
然后依次作用在非线性图上
注:正如前文所说,在点击invert后这个拉伸函数将与原来的函数互为反函数,因此不能打乱其与图片作用的顺序,否则将无法得到“线性图”。
自此已经达到我们的目的,获得一张去星良好的“线性图”。



(使用STF预览的效果)


(即使经过强烈拉伸也基本没有星点光晕的痕迹)
若想获得星点图则可以从历史记录中拖出最开始的图,使用Pixelmath减去去星后的图,得到星点图。
最后来一波对比:
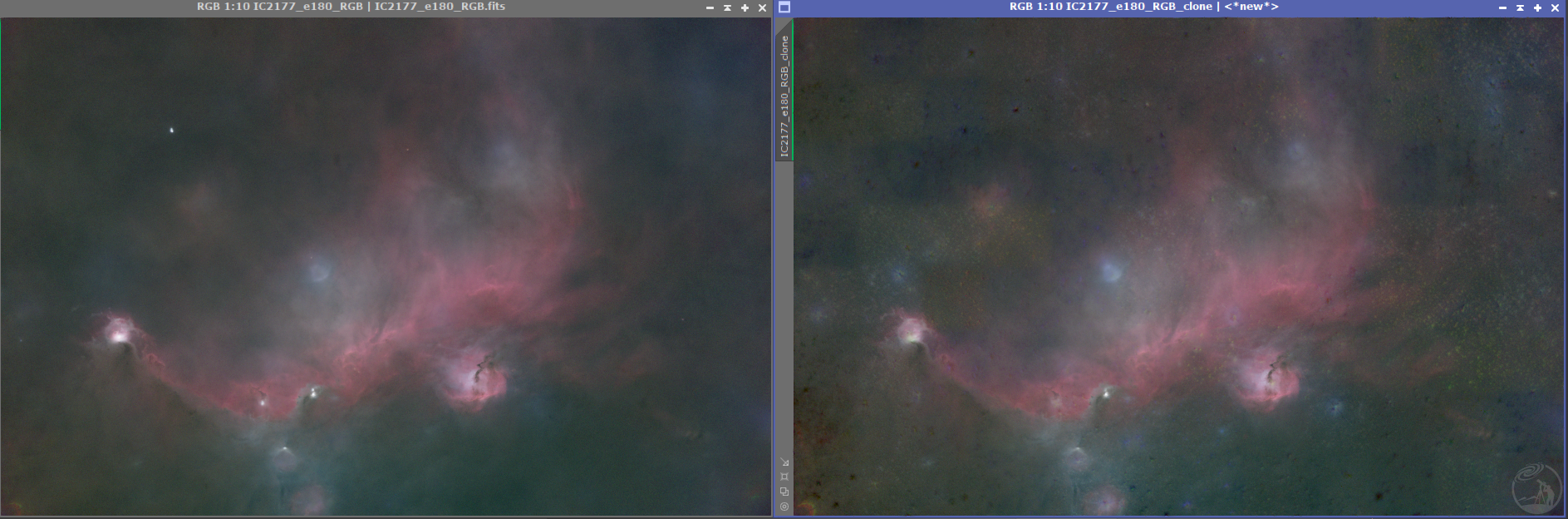
(左图为使用本文的方法,右图为直接线性状态去星的结果,使用同一个STF)
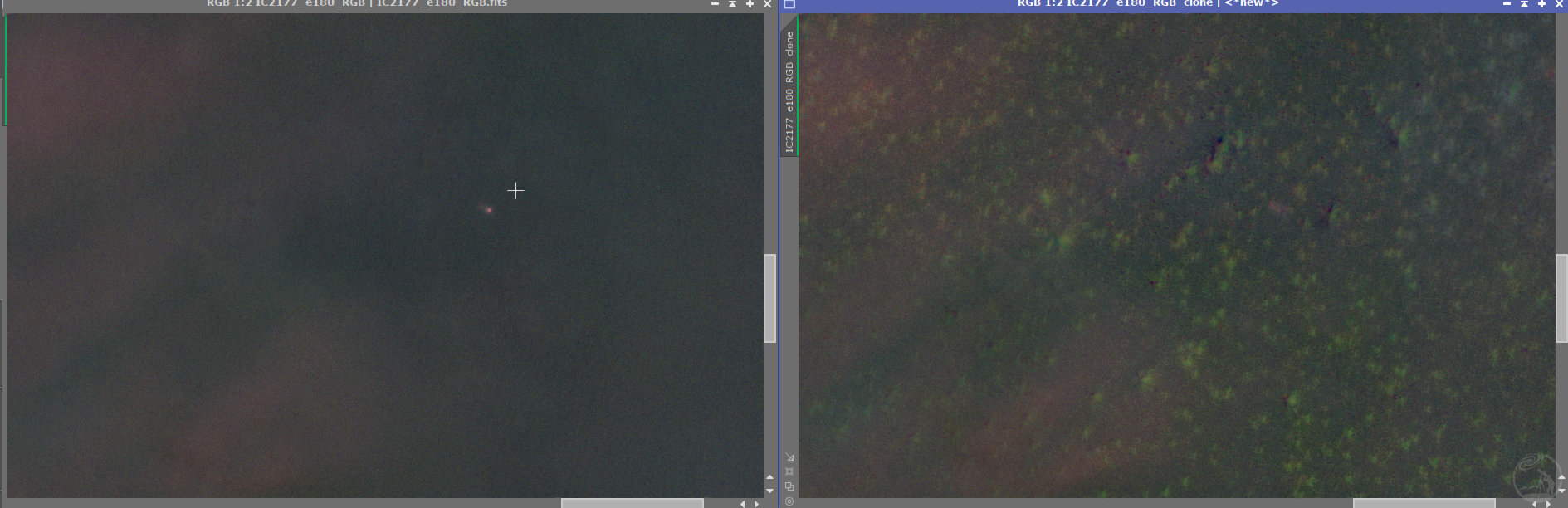
(同一区域对比,使用同一个STF)
可见效果是很明显的。
三、总结
此方法最主要依靠的就是SXT在非线性状态下的使用,作者没有尝试过starnet,因此不敢保证是否能将SXT替换。
流程不涉及蒙版的制作,适用性比较广,(作者本人作品中就有两版海豚星云,其区别还是很明显的),但最终效果跟使用者的拉伸手法有很大关系,作者本人建议少次,且猛烈的拉伸,但在切除时应注意不应切除过多数据。
此方法也能避免SXT的AI将一些非星点的结构识别成结构而误去除。

星友评论