拍摄在轨运行的空间站是天文摄影中极具挑战性的目标。其高速运动、较小的视尺寸，以及对光学系统分辨率的严苛要求，使得普通摄影设备难以捕捉细节。本文将系统解析空间站的轨道参数与视尺寸关系，推导光学设备的最小口径需求，并给出相机与光学系统的相对合理协同优化方案。
一、空间站的尺寸
（一）中国空间站
1.总长度（组合体）约 55米，包含天和核心舱（长度16.6米、直径4.2米） 、问天实验舱（长度17.9米、直径4.2米） 、梦天实验舱（长度17.9米、直径4.2米）、神州载人飞船（长度9米、直径2.8米，对接后突出长度约1.5米）、天舟货运飞船（长度10.6米、直径3.35米，对接后突出长度约2米）。
2. 最大宽度约 40米（两侧柔性太阳翼完全展开时）
（二）国际空间站
网查国际空间站（ISS）总长度约为109米，总宽度约为73米（桁架跨度）。
（三）空间站视尺寸的简易计算
在天文观测中，我们一般采用视尺寸来表示天体的大小，他指的是天体在观测者视角中所占据的角度大小，我们也经常称之为天体的角直径或视直径。当被观测天体与地球的距离 （D） 远大于天体自身的物理直径（d）时，天体的视尺寸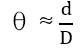
（此时单位为弧度，我们要将其转化为角度）。
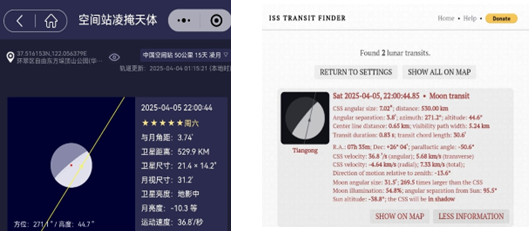
参照左图，我们假设空间站的卫星距离（此时的卫星距离为斜距，我们在下文解释）为529.9km，中国空间站的尺寸为55*40m。
基本与左图卫星尺寸21.4*14.2″相同。
在右图的ISS Transit Finder中，CSS给出的尺寸为7.02″，这个尺寸明显与之前计算的差异很大，猜测可能是按照天和核心舱（长度16.6米、直径4.2米）的数据进行计算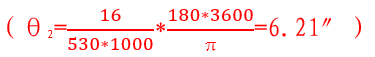
。
二、空间站的轨道高度及速度
1.轨道高度。中国空间站的轨道高度约为380-450公里，国际空间站的轨道高度约为400公里。当我们通过各种天文软件获取空间站过境信息时我们会发现有时的“空间站距离”远大于轨道高度，其实此 “距离”为空间站的“斜距”，斜距是软件通过空间站的轨道参数及观察者所在地区的经纬度计算出来的观测者与卫星之间的直线距离，因此斜距会因空间站的运动及轨道高度的变化、观测者位置、地球的自转等因素动态改变。
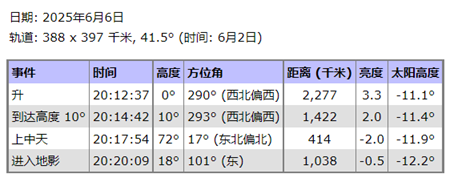
2.速度。空间站的速度分为线速度和角速度，由于空间站轨道为近圆轨道，速度变化幅度很小，排出外在因素短周期内可视为近似恒定。但斜距影响了观察者视角中的速度，斜距越小，视直径越大，同时空间站的亮度也会增加，所以“相对小的斜距”是我们拍摄的理想选择。
三、光学系统的分辨率
1. 光学系统的角分辨率衍射公式光学系统的角分辨率由光学系统的口径决定的，且受衍射限制。由于光具有波动性，衍射效应限制了光学系统分辨率，即使是理想光学系统，点光源也会因圆孔衍射变成一个弥散斑，圆孔的零级衍射斑就是艾里斑，其大小直接决定了分辨极限。我们熟悉的瑞利判据θ＝1.22 λ/d ，就是基于光的衍射理论，给光学系统规定的一个最小分辨角标准。
2.光学系统中的口径“D”
在光学系统中，由若干反射面或折射面组成的光学系统我们称之为光具组，而真正决定通过光具组光束孔径的光阑称之为孔径光阑，孔径光阑也被称之为有效光阑。在望远镜系统中，望远镜的口径也就是孔径光阑，也是我们文中提到的“D”。
而在单反镜头中孔径光阑与镜头的口径却不是一个概念。单反镜头的孔径光阑需要利用光圈值和焦距进行计算。首先光圈值在镜头中其实有两种表达方式，一种是使用“F值”来表示，另一种使用“T值”（电影镜头）。区别在于F值为镜头的几何表达方式，或者称之为几何光圈。T值则是考虑了镜头光学损耗（镀膜、镜片数量等），T值更能反映出镜头实际的透光率及真实透光量。其实无论是F值还是T值，对我们计算孔径光阑影响都不会太大，当我们知道镜头的F值或T值、镜头焦距时，此时镜头的孔径光阑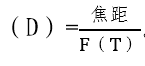
。
3.光学系统的角分辨率的几何公式
在“空间站视尺寸的简易计算”中，我们提过天体的视尺寸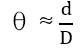，就是从简单的几何关系推到出来的，本质是被观测目标的分辨率。从物面几何角度看
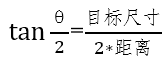，当θ无限小时，
（单位：度）。
4.瑞丽判据与几何公式的应用
结合瑞丽判据及物面几何公式，我们推导出D（光学系统的孔径光阑）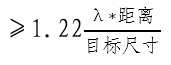
。
假设要分辨空间站上1m结构，观测地点的空间站斜距为400km，λ取550 nm，暂抛开视宁度的影响，
。
四、相机
（一）像元尺寸
相机的像元尺寸（即单个像素的物理尺寸）直接影响分辨率、信噪比。大像元的高感、信噪比更好，但分辨率会相应降低。小像元分辨率更高、细节丰富，但信噪比低，且需要强光照。所以像元尺寸直接影响图像细节、捕捉能力及信噪比等。
（二）像元分辨率与艾里斑线半径
1.像元分辨率
像元分辨率=底片比例尺*像元尺寸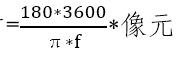
（单位：角秒/像素）。
2.艾里斑线半径艾里斑线半径是其在成像平面（相机）上的实际物理半径。根据艾里斑公式
（θ为角半径单位：角秒），如果成像系统焦距为 f，则艾里斑在像面上的实际物理半径为 
。
3.艾里斑与艾里斑线半径
参照艾里斑
和线半径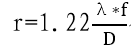
公式，我们可以知道，一是光学系统的分辨率θ仅取决于口径 D和波长λ，与焦距 f 无关。二是两个公式带入替换后r=θ *f，由此可知艾里斑在成像平面上的实际物理半径r，由艾里斑θ和焦距 f 共同决定，焦距f为艾里斑角半径θ的“显示尺度”，当焦距越长时，艾里斑的实际半径成像被“放大”， 但角分辨率θ不变。所以使用同口径而不同焦距的望远镜，只是改变了成像尺寸，而我们想分辨的“目标尺寸”并未改变。
4.光学系统的合理“放大”
根据r=θ *f，我们在同口径不改变光学系统分辨本领的前提下，通过延长焦距f来放大视角，那么这个焦距多大合适？在望远镜目视系统中，我们知道放大率
但是通常也会有一个限制，最大有效倍率通常不超过望远镜口径的2倍。以上是因为在光学系统中，所有的图像都是我们的眼睛对信息的反馈，所以最小分辨角只能放大到人眼所能分辨的最小角度。
我们眼睛瞳孔直径D基本在2-8mm之间调节，根据，使光学系统的最小分辨角放大到人眼所能分辨的最小角度的放大率
。所以f并不是可以做到无限大，是需要同我们的眼睛相互匹配。
（三）像元尺寸与光学系统的匹配
像元尺寸需与光学系统的角分辨率相互匹配，像元尺寸决定了空间采样频率。根据奈奎斯特采样定理，采样频率需至少为光学系统最高空间频率（由光学镜头分辨率决定）的两倍。
根据采样定理，
即r≥2*像元分辨率，带入得出2*像元尺寸
。
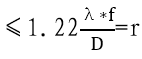当像元尺寸
，此时为相机和光学最佳平衡状态。
当像元尺寸
，此时相机过采样，分辨率受限于光学系统，但可提升信噪比。像素合并Binning（Bin）此时就可以考虑应用上了。
当像元尺寸
，此时相机采样不足，浪费了光学系统的性能。此时如果我们可以在光学系统上使用增倍镜，增加线半径r，以此来平衡相机与光学系统的状态。
五、视宁度的影响
在地面观测中，视宁度是衡量大气湍流对天文观测影响的指标，表示星光通过地球大气时因折射率不均匀导致的图像抖动和模糊程度以及大气抖动对光学成像的影响程度。大气湍流通常使星点扩散至1-2″（甚至更大），视宁度1″表示星点因大气扰动扩散成1″大小的光斑，此时的星点大小可能大于望远镜的理论分辨率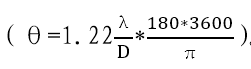
。
1.当星点大小因视宁度的影响大于望远镜的理论分辨率时，像元尺寸应与星点的扩散值相互匹配。根据采样定理
，结合像元分辨率此时像元尺寸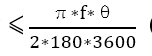
（θ为当前视宁度下的星点大小）。
2.当星点大小因视宁度的影响小于望远镜的理论分辨率时，像元尺寸应与望远镜理论分辨率相互匹配。
六、空间站剪影摄影
空间站凌日（月）摄影大部分（由于月相的变化，我们在清晨或者傍晚时分拍摄的空间站凌月就不属于剪影）还是属于剪影摄影，剪影摄影只突出主体轮廓，而隐藏细节（影子无法表现细节）。那么我们拍空间站凌日（月）时，只要能保证空间站轮廓清晰、有较高的辨识度基本就是一副好的作品了。上文中的“光学系统的口径”可能就显得不是那么的重要了。
从喜欢上天文到现在也有两三年的时间了，在这几年的时间里，从未有过一副可以拿出手的天文作品。好在一直没有放弃对天文喜爱，本文以收集、整理的方式将空间站拍摄中所需要的天文知识进行归纳、总结。写这篇文章的初衷是为了拍出更清晰的空间站，后知后觉中发现一直忽略了一个问题，我之前拍的都是空间站的“剪影”。真正空间站的拍摄由于赤道仪和跟踪程序的原因从未实践过，大家且把它当成“纸上谈兵”，即使是“纸上谈兵”也希望广大同好能帮助指正错误、提出疑议，我好及时修正。
星友评论